I present Grz.2 is complete for Finite Boolean Algebras, a draft of my upcoming paper on the subject of modal logic and Kripke semantics. In this work, I provide an accessible exposition of the Grzegorczyk axiom and give a new characterization of the modal logic Grz.2.I provide a new interpretation of the Grzegorczyk axiom and show that the modal logic Grz.2 is characterized by finite Boolean algebras.
From Mishap to Marvel: The Unintended Discovery
Let me start with some history. The story begins with a big announcement of a (false) theorem that Joel David Hamkins and I proved (we thought we did but we did not).
Just before a formal announcement at an event in Amsterdam, Joel found a flaw in our argument. But the “great news” have remained on the slides online. And so a MathOverflow thread ensued, where Joel finally published a retraction. This has left everyone with an open question: for what upper bound on the modal validities do buttons actually suffice? Ultimately, at the beginning of my DPhil at the University of Oxford, I showed that the answer is Grz.2. I presented the result at the National University of Singapore in 2022, and additionally shared some details on MathOverflow beforehand.
The draft of the paper I am presenting to you today is key in demonstrating that buttons are sufficient for the upper bounds to be Grz.2. It includes a proof of this fact for propositional Kripke models. The relevant arguments are easily adaptable to the case of any arbitrary potentialist system or a Kripke category, with details appearing in my pre-print The modal theory of the category of sets.
The Grzegorczyk axiom
At first glance, the Grz axiom is very scary. It says that if always it is the case that if always we have that p implies that always p, then p, then p.
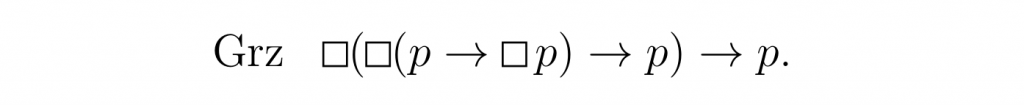
However, I provide an easy understanding of the axiom by introducing the concept of penultimacy of p: the truth-value of p is false but if it ever flips, it will never flip again—thus staying necessarily true from that point on. The Grzegorczyk axiom simply says that p is either true or possibly penultimate.
The modal logic Grz.2
The modal logic Grz.2 is the smallest normal modal logic that contains the axiom Grz and the axiom .2, which says that everything that is possibly necessary is also necessarily possible.
Abstract. The article offers an accessible exposition of the Grzegorczyk axiom and provides a new characterization of the modal logic Grz.2, establishing that it is complete for the set of finite Boolean algebras. Thereby, it enhances the utility of the control statement technique of establishing upper bounds on the modal validities of a potentialist system [HL08; HL19; HW20].
Note that this draft is subject to revision and change. Feedback and comments are always welcome!
